From the exercise we know that there are 20 people, that 7 are men and 13 are women if only one is going to choose and one we must multiply their combinations
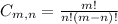
For males we have
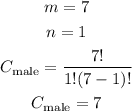
For females we have
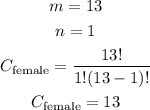
Now we multiply the combinations to know how many options the director has to choose his actors
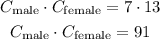
The answer is there are 91 ways to audition.