Question

What are the answers from Step A through Step C?

Answer 1

Given:

`y=-0.32x^2+35.05x+5832.82`

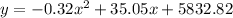
Where (x) is the number of years after 1990 and (y) is the population of the people.

A) Find the input and the output at the vertex of the graph.

The vertex has the following coordinates:

`\begin{gathered} x-coordinate=(-b)/(2a)=(-35.05)/(2(-0.32))\approx54.77 \\ y-coordinate=-0.32(54.77)^2+35.05(54.77)+5832.82\approx6792.59 \end{gathered}`

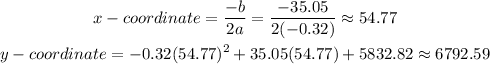
So, the answer will be:

The input at the vertex is x = 54.77 and output at y = 6792.59

=========================================================

(B) Interpret the values from A

After about 55 years that will be in 2045, the population of the people will be around 6793

==========================================================

(C) For what year after 1995 does this model predict that the population will increase?

As shown from the vertex at x = 55

So, the population will increase till the year = 1990 + 55 = 2045

the number of years from 1995 to 2045 will be as follows:

`2045-1995=50`

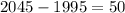
So, the answer will be 50 years