We have the cost function for x units as:

a) We can find the marginal cost as the first derivative of the cost function:

b) We can find the marginal cost when x = 100 by replacing x with 100 in the marginal cost function:
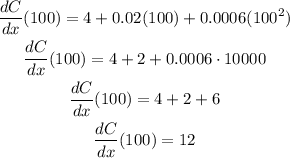
c) To calculate the cost at x = 100, we replace x with 100 in the cost function and calculate:
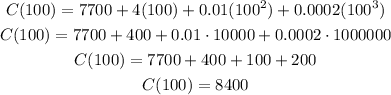
Answer:
a) 4 + 0.02x + 0.0006x²
b) 12
c) 8400