We are given
Initial Population = 300,000
Rate of increasing per year = 3% = 0.03
We want to find the population at time t = 22 years
Solution
The formula to use the formula for the compound interest given as
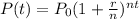
Here
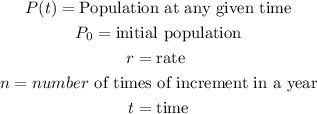
Thus, we want to find P(22)
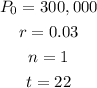
Substituting into the formula we have
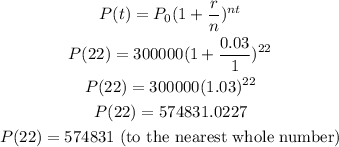
Therefore, the population in 22 years time will be 574,831