We have a segment AB, of which we know the coordinates of one endpoint A=(-2,-8) and the midpoint M=(2,-7).
We can relate the x and y coordinates of the endpoints and the midpoints as:
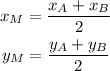
The coordinates of the midpoints are the average of the coordinates of the endpoints.
As we know the coordinates of A and M, we can calculate the coordinates of B as:
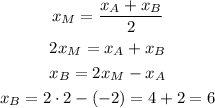
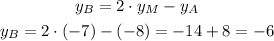
Answer: the coordinates of B are (6, -6)