Question

A rectangle has a length of of ( 2.3 +-0.2) m and a width of (1.2+-0.2) Calculate the area and the perimeter of the rectangle and give the uncertainty In each value

Answer 1

Remember that if x and y are two measurements:

`\begin{gathered} x=x_0\pm\delta x \\ y=y_0\pm\delta y \end{gathered}`

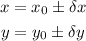
Then, the uncertainty in the sum and the product of x and y are given by:

`\begin{gathered} x+y=(x_0+y_0)\pm(\delta x+\delta y) \\ x\cdot y=(x_0\cdot y_0)\pm(x_0\cdot\delta y+y_0\cdot\delta x) \end{gathered}`

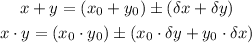
Additionally, the uncertainty of a constant multiplied by a measurement is given by:

`kx=kx_0\pm k\cdot\delta x`

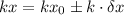
The perimeter and the area of a rectangle with dimensions L and W are:

`\begin{gathered} P=2(L+W) \\ A=L\cdot W \end{gathered}`

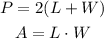
Replace L = ( 2.3±0.2) m and W = (1.2±0.2)m to find the perimeter and the area of the rectangle with the corresponding uncertainty:

`\begin{gathered} P=2\left(\left[2.3±0.2\right]+\left[1.2±0.2\right]m\right) \\ =2\left(\left[2.3+1.2\right]\pm\left[0.2±0.2\right]\right)m \\ =2(3.5\pm0.4)m \\ =(7.0\pm0.8)m \end{gathered}`
`\begin{gathered} A=(2.3±0.2)m\cdot(1.2±0.2)m \\ =(\lbrack2.3\cdot1.2\rbrack\pm\lbrack1.2\cdot0.2+2.3\cdot0.2\rbrack)m^2 \\ =(2.76±\lbrack0.24+0.46\rbrack)m^2 \\ =(2.76±0.7)m^2 \end{gathered}`

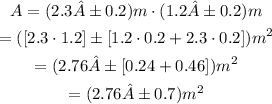
Therefore, the area and the perimeter of the rectangle are:

`\begin{gathered} A=(2.76±0.7)m^2 \\ P=(7.0±0.8)m \end{gathered}`