For this case we know that the Moon orbits the Earth in a circular orbit at a distance of about 240000 miles, we also know that for one complete trip it takes about 27.3 days and we want to estimate the average velocity in km/hr
The first step here is convert the miles into km and the days into hours and we got this:
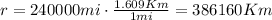
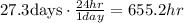
After this we know that the total circumference of a circle is given by:
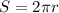
And from here is possible to find the distance covered in one orbit:

And then we can use the definition of velocity given by:
![v=(S)/(t)=(2426314.838Km)/(655.2hr)=3703.167\operatorname{km}/hr]()
So for this case we can conclude that the average velocity for the Moon is given by 3703.167 Km/hr