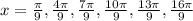Question

Use trigonometric identities and algebraic methods, as necessary, to solve the following trigonometric equation. Please identify all possible solutions by including allanswers in [0,2) and indicating the remaining answers by using n to represent any integer. Round your answer to four decimal places, if necessary. If there is nosolution, indicate "No Solution."sin(3x) = V3cos(3x)

Answer 1

Given the equation:

`\sin (3x)=\sqrt[]{3}\cos (3x)`

Let's find all possible solutions over the interval:

`\lbrack0,2\pi)`

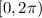
Let first simplify the equation.

Divide both sides by cos(3x):

`\begin{gathered} (\sin3x)/(\cos3x)=\frac{\sqrt[]{3}\cos (3x)}{\cos 3x} \\ \\ (\sin 3x)/(\cos 3x)=\sqrt[]{3} \end{gathered}`

Apply the trigonometric identity:

sinx/cosx = tanx

We have:

`\tan 3x=\sqrt[]{3}`

Take the inverse tangent of both sides:

`\begin{gathered} 3x=\tan ^(-1)(\sqrt[]{3}) \\ \\ 3x=(\pi)/(3) \end{gathered}`

Divide both sides by 3:

`\begin{gathered} (3x)/(3)=(\pi)/(3)*(1)/(3) \\ \\ x=(\pi)/(9) \end{gathered}`

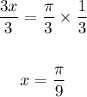
The tangent function is positive in the first and third quadrant. Let's find the second solution by adding π to the reference angle:

`\begin{gathered} 3x=(\pi)/(3)+\pi \\ \\ 3x=(\pi+3\pi)/(3) \\ \\ 3x=(4\pi)/(3) \\ \\ x=(4\pi)/(9) \end{gathered}`

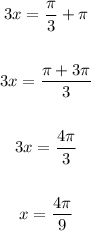
Let's find the period of tan(3x):

`(\pi)/(b)=(\pi)/(3)`

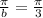
Since the period is π/3, the solution values will repeat every π/3 in both directions.

We have:

`x=(\pi)/(9)+(\pi n)/(3),(4\pi)/(9)+(\pi n)/(3)`

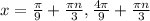
When n = 1:

`x=(\pi)/(9)+(\pi)/(3)=(4\pi)/(9)`

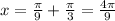
When n = 2:

`(\pi)/(9)+(2\pi)/(3)=(\pi+6\pi)/(9)=(7\pi)/(9)`

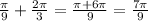
WHen n = 3:

`(\pi)/(9)+(3\pi)/(3)=(10\pi)/(9)`

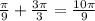
When n = 4:

`(\pi)/(9)+(4\pi)/(3)=(\pi+12\pi)/(9)=(13\pi)/(9)`

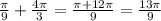
When n = 5:

`(\pi)/(9)+(5\pi)/(3)=(\pi+15\pi)/(9)=(16\pi)/(9)`

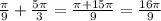
Therefore, the solutions are:

`x=(\pi)/(9),(4\pi)/(9),(7\pi)/(9),(10\pi)/(9),(13\pi)/(9),(16\pi)/(9)`

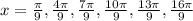
ANSWER:

`x=(\pi)/(9),(4\pi)/(9),(7\pi)/(9),(10\pi)/(9),(13\pi)/(9),(16\pi)/(9)`