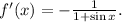Question

How to solve these Trigonometry functions without using chain rule for any of them. Problem 3.

Answer 1

3.- To answer this question, we will use the quotient rule:

`((f(x))/(g(x)))^(\prime)=\frac{g(x)f^(\prime)(x)-f^{}(x)g^(\prime)(x)}{(g(x))^2}.`

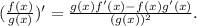
Before applying the rule, we will determine each derivative to avoid confusion:

`\begin{gathered} (\cos x)^(\prime)=-\sin x, \\ (1+\sin x)^(\prime)=(1)^(\prime)+(\sin x)^(\prime)=0+\cos x=\cos x. \end{gathered}`

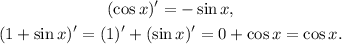
Now, we substitute the above results in the quotient rule:

`f^(\prime)(x)=((1+\sin x)(-\sin x)-(\cos x)(\cos x))/((1+\sin x)^2).`

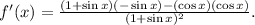
Simplifying the above result, we get:

`f^(\prime)(x)=(-\sin x-\sin ^2x-\cos ^2x)/((1+\sin x)^2).`

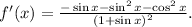
Recall that:

`\sin ^2x+cos^2x=1.`

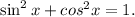
Therefore:

`f^(\prime)(x)=(-\sin x-1)/((1+\sin x)^2)=(-(\sin x+1))/((1+\sin x)^2)=-(1)/(1+\sin x).`

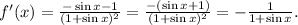
Answer:

`f^(\prime)(x)=-(1)/(1+\sin x).`