Question

Fill in the table with the missing values of a, b, c, and d.

Answer 1

We need to find the values of the missing integers uisng factorization:

1.

`x^2-8x+15=(ax+b)(cx+d)`

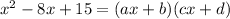
We need to factor the trinomial.

First, look at the sign of the expression

The first sign = -

The second sign = +

Now, we need to square root the first term x² = √x² =x.

Then, we use the parentheses ( ) ()

We put the result of the square root

(x )(x)

Then, we use the first sign (in this case is -) in the first parentheses and the multiplication of both signs (in this case -*+ = -) in the second parentheses:

(x- )(x-)

Finally, we need to find both numbers that multiply by each other the result is 15 and they add up to 8

Hence;

3*5 = 15

5+3=8

So, the result of the factoring is:

(x-5)(x-3)

Where

(ax+b)(cx+d).

So d = -3

2.

`2x^3-8x^2-24x=2x(ax+b)(cx+d)`

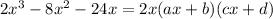
First, we can factor finding their common term:

In this case, is 2x. Hence we can write the equation as:

`2x^3-8x^2-24x=2x(x^2-4x-12)`

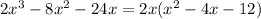
Now, we have the form ax²+bx+c

Find the product of ac= (1)(-12)= -12

Then, find two factors of ac that have a sum equal to b :

Then:

2-6 = -4

Rewrite the trinomial:

`x^2-4x-12=x^2+2x-6x-12`

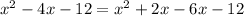
Use the factor by grouping:

`\begin{gathered} x^2+2x-6x-12=x(x+2)-6(x+2) \\ \text{Factor again} \\ x(x+2)-6(x+2)=(x+2)(x-6) \\ \text{Therefore:} \\ 2x^3-8x^2-24x=2x(x+2)(x-6) \end{gathered}`

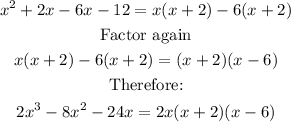
Using the given expression:

`2x(ax+b)(cx+d)=2x(x+2)(x-6)`

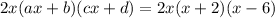
Therefore:

b=2

c=1

3.

`\begin{gathered} 6x^2+14x+4 \\ \end{gathered}`

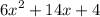
We have an expression with the form ax²+bx+c.

First, find the product of ac:

ac= 6*4 =24

Find two products of ac that have a sum equal to b.

Factors/ products

(12)(2)= 24 / 12+2 = 14

Hence, we can rewrite the trinomial as:

`\begin{gathered} 6x^2+14x+4=6x^2+12x+2x+4 \\ Factor\text{ by grouping:} \\ 6x^2+12x+2x+4=6x(x+2)+2(x+2) \\ \text{Factor by grouping again:} \\ (6x+2)(x+2) \\ or\text{ we can write as:} \\ (3x+1)(2x+4) \end{gathered}`

Where a= 3 and d=4