Let's use the variable x to represent the amount of $6 candy bought and y to represent the amount of $9 candy bought.
If the final mixture has 15 pounds, we have the equation:
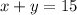
Then, the final price is $7 per pound, so we can write the equation:
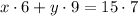
Solving this system, we have:
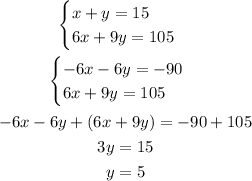
So the number of pounds of the expensive candy if 5, therefore the correct option is A.