Question

4. The diameter of a circle has endpoints P(-6,-11 ) and Q(4,7).Write an equation for the circle. Be sure to show and explain all work.

Answer 1

- The endpoints of the diameter are P(-6, -11) and Q(4, 7).

- The formula for the equation of a circle is:

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ where, \\ (a,b)\text{ is the center of the circle} \\ r\text{ is the radius of the circle} \end{gathered}`

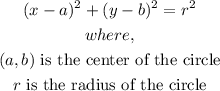
- To find the radius of the circle, we need to find the coordinate of the center and then apply the distance formula to find the length of the radius.

- That is,

`\begin{gathered} \text{ Midsegment of a line or the coordinates of the middle of two points:} \\ M(x,y)=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ \\ \text{ Distance between two points:} \\ \bar{D}=√((x_2-x_1)^2+(y_2-y_1)^2) \end{gathered}`

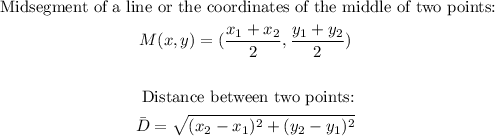
- Applying the midsegment formula given above, we can find the coordinates of the center of the diameter as follows:

`\begin{gathered} Given,\text{ \lparen-6,-11\rparen and \lparen4,7\rparen} \\ M(x,y)=((-6+4)/(2),(-11+7)/(2)) \\ \\ M(x,y)=(-1,-2) \end{gathered}`

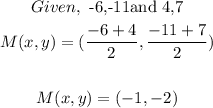
- Thus, the coordinate of the center of the circle is:

`\begin{gathered} (-1,-2) \\ \\ \text{ Thus, we can say,} \\ (a,b)=(-1,-2) \\ \\ \text{ That is,} \\ a=-1,b=-2 \end{gathered}`

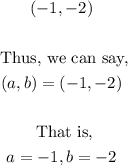
- Now that we have the coordinates of the center, we can find the distance from the center to any of the points given to us that lie on the circumference of the circle using the distance formula given above. This will give us the radius.

- Thus, we have:

`\begin{gathered} \text{ The distance between \lparen-1, -2\rparen and \lparen4,7\rparen is:} \\ r=√((7-(-2))^2+(4-(-1))^2) \\ \\ r=√(9^2+5^2) \\ \\ r=√(81+25) \\ \\ r=√(106) \end{gathered}`

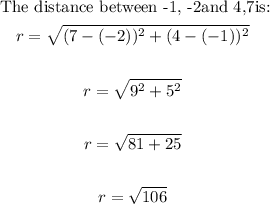
- Thus, we can write the equation of the circle as follows:

`\begin{gathered} (x-(-1))^2+(y-(-2))^2=(√(106))^2 \\ \\ (x+1)^2+(y+2)^2=106 \end{gathered}`

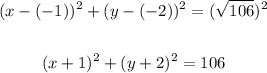
The circle is depicted below: