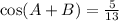Given
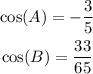
To evaluate:
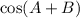
Use the identity:
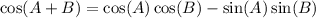
To get sin(A):
Using the trigonometric ratios:
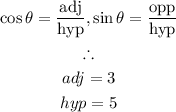
Using the Pythagorean Theorem, we have:
![\begin{gathered} opp^2=hyp^2-adj^2 \\ opp^2=5^2-3^2 \\ opp^2=25-9 \\ opp^2=16 \\ opp=\sqrt[]{16}=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wpt12nay2uf3c3nljya0r04hzizzstf4hl.png)
Hence,
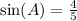
Since A is in Quadrant III,
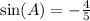
To get sin(B):
Using the trigonometric ratios:
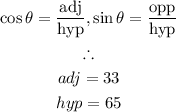
Using the Pythagorean Theorem, we have:
![\begin{gathered} opp^2=hyp^2-adj^2 \\ opp^2=65^2-33^2 \\ opp^2=4225-1089 \\ opp^2=3116 \\ opp=\sqrt[]{3116}=56 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rn71b8z59v8bdcqq776owhrqd7neuahv2j.png)
Hence,
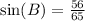
To Evaluate cos (A + B):
Recall:
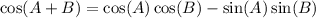
Inputting all the necessary values, we have:
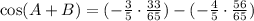
Using a calculator, we have the answer to be: