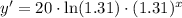Remember the following properties of the derivatives:
Derivative of an exponential function:
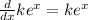
Chain rule:
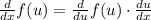
Also, remember the following property of exponentials:
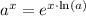
Use these properties to find the derivative of the following function:
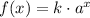
The function can be rewritten as:
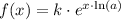
Let:
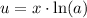
Then:
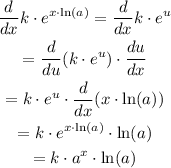
In this case, we can see that k=20 and a=1.31:
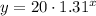
Then, the derivative of this function, is:
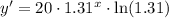
Therefore, the rate of increase of the given function, is: