SOLUTION
We were given that
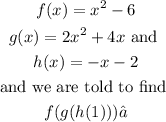
Firstly, we have to find g(h(x)). This means plugging in h(x) into g(x). Doing this we have
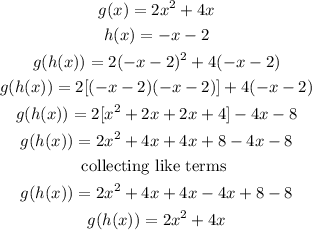
Next, we plug in g(h(x)) into f(x), we have
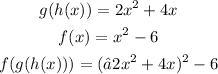
No need to expanding that, as this would be time wasting, now let's find f(g(h(1))). To do this, we substitute 1 for x in f(g(h(x))), we have

Hence the answer is 30