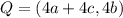From the figure, we know that segments PQ and SR have the same lenght and they are parallel. This implies that the y-coordinate of Q is
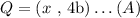
Now, in order to find the x-coordinate of Q, we must use the fact that
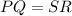
this implies that
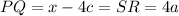
Therefore, x is given by
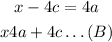
Then, from equations A and B, the point Q is given by