In order to calculate the probability of each item, we need to use a combination formula.
The combination of n choose p elements can be calculated with the formula below:
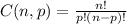
For the beverages, she will choose 3 items among 18 options, so the number of ways she can choose is:
![C(18,3)=(18!)/(3!15!)=\frac{18\cdot17\operatorname{\cdot}16}{3\operatorname{\cdot}2}=816]()
For the appetizers, she wants 2 items among 8 options, so:
![C(8,2)=(8!)/(2!6!)=\frac{8\operatorname{\cdot}7}{2}=28]()
For the desserts, she will choose 2 items from 5 options, so:
![C(5,2)=(5!)/(2!3!)=\frac{5\operatorname{\cdot}4}{2}=10]()
Now, calculating the total number of possibilities, we have:
![\begin{gathered} N=C(18,3)\operatorname{\cdot}C(8,2)\operatorname{\cdot}C(5,2)\\ \\ N=816\operatorname{\cdot}28\operatorname{\cdot}10\\ \\ N=228480 \end{gathered}]()