Question

The constant of proportionality for a proportional relationship is 5. Circle all of the points below that would lall on the line representing this proportional relationship. (5,1) (3, 15) (10,2) (0.5)

Answer 1

The proportional relation between two variable with constant of proportionality equal to 5 is,

`y=5x`

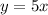
For x = 5,

`\begin{gathered} y=5\cdot5 \\ =25 \end{gathered}`

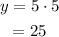
(5,1) not lies on the line as for x = 5, the y is 25.

For x = 3,

`\begin{gathered} y=5\cdot3 \\ =15 \end{gathered}`

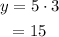
The point (3,15) lies on the line.

For x = 10

`\begin{gathered} y=5\cdot10 \\ =50 \end{gathered}`

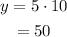
Point (10,2) not lies on the line.

For x = 0,

`\begin{gathered} y=\text{ 5}\cdot0 \\ =0 \end{gathered}`

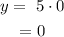
The point (0,5) not lies on the line.

So point (3,15) lie on the line.