We can model Max's income through an equation >>
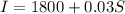
Where
"I" is his total income (fixed salary of 1800 and 3% commission on sales)
"S" is the total amount of sales he does
Note: 0.03 is the decimal form of 3%
We are given that "he needs an income of 3000" . So, I = 3000.
We need to know the "sales" amount for this income, thus, we need to find "S".
Let us substitute I = 3000 and solve for "S". The steps are shown below:
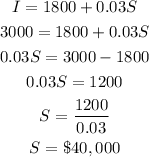
Thus, Max needs to sell $40,000 in order for his total income to be $3000.
Answer$40,000