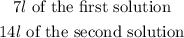Question

Used two equations in two variables to solve the application.A chemist has one solution that is 40% alcohol and another that is 55% alcohol. How much of each in liters must she used to make 21 L of a solution that is 50% alcohol.

Answer 1

Given that the chemist has one solution that is 40% alcohol and another that is 55% alcohol.

We can find how much of each in liters must she used to make 21 L of a solution that is 50% alcohol below.

Since we don't have the quantity of each solution of the alcohol we would be mixing, we would assume the following.

`\begin{gathered} solution1\text{ 1=x} \\ \text{solution 2 =}(\text{21-x)} \end{gathered}`

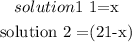
Therefore, we would have

`\begin{gathered} (40)/(100)x+(55)/(100)(21-x)=(50)/(100)*21 \\ 0.4x+0.55(21-x)=0.5*21 \\ 0.4x+11.55-0.55x=10.5 \\ -0.15x=10.5-11.55 \\ -0.15x=-1.05 \\ x=(-1.05)/(-0.15) \\ x=7 \end{gathered}`

Since x =7, we would then get the quantity of each alcohol as

`\begin{gathered} solution1\text{ 1=}7l \\ \text{solution 2=}(21-7) \\ =14 \end{gathered}`

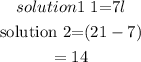
Therefore, the answer is

`\begin{gathered} 7l\text{ of the first solution} \\ 14l\text{ of the second solution} \end{gathered}`