Question

Find the function with the given derivative whose graph passes through the point P.r'(theta)=9+sec^2(theta), P(pi/4,2)

Answer 1

The given derivative is:

`r^(\prime)(\theta)=9+\sec ^2\theta`

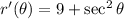
Integrate w. r. t. theta to get:

`\begin{gathered} r(\theta)=\int (9+\sec ^2\theta)d\theta \\ =9\int d\theta+\int \sec ^2\theta d\theta \end{gathered}`

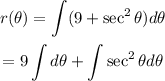
Use the formulae given by:

`\int d\theta=\theta+c,\int \sec ^2\theta d\theta=\tan \theta+c`

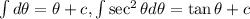
To get the solution as follows:

`r(\theta)=9\theta+\tan \theta+c`

The given point is P(pi/4,2) so it follows:

`\begin{gathered} 2=9((\pi)/(4))+\tan (\pi)/(4)+c \\ 2-(9\pi)/(4)-1=c \\ c=1-(9\pi)/(4) \end{gathered}`

Substitute the value to get the required answer as follows:

`r(\theta)=9\theta+\tan \theta+1-(9\pi)/(4)`

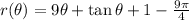
The above function is the required answer.