It is stated in the problem that the quadrilateral given is composed of two triangles. What can we do here to find the area of the quadrilateral is to find the area of the two triangles via Heron's formula then the sum of the area of the triangles will be the overall area of the quadrilateral. Heron's formula is
![A=\sqrt[]{s(s-a)(s-b)(s-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/t3rmhsk71nltcmgtu237bvtgrmrx89v4xv.png)
where a, b, and c are the sides of the triangle while s is the semi-parameter of the triangle, which is computed as
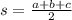
Let's compute first for the triangle on the left side of the quadrilateral. We have
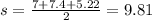
![\begin{gathered} A=\sqrt[]{9.81(9.81-7)(9.81-7.4)(9.81-5.22)} \\ A=17.46 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ulhmjc0xyort6dm7rc8f3khoi6eafrx1s0.png)
For the second triangle, which is on the right side of the quadrilateral, we have
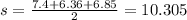
![\begin{gathered} A=\sqrt[]{10.305(10.305-7.4)(10.305-6.36)(10.305-6.85)} \\ A=20.20 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/l70g3g9lsyzi9gjx8b63sl0t2h63rmin4z.png)
Summing up the area of these triangles, we get
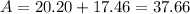
Therefore, the area of the quadrilateral given is equal to 37.66 units^2.
Answer: B. 37.66 units^2