Question

Harper just lit a new candle and then let it burn all the way down to nothing. Thelength of the candle remaining unburned, in inches, can be modeled by the equationL=15 - 1.5t, where t represents the number of hours since the candle was lit. What is the slope of the equation and what is its interpretation in the context of the problem?The slope of the function is ___ which reveals (the number of hours the until the candle burned fully, the original length of the new candle, the number of inches of candle that burns per hour, or the total number of candle inches that have burned).

Answer 1

The equation of the burning candle can be modelled as:

`L=15-1.5t`

In order to interpret this equation, we first need to understand the slope-intercept form of a line. The form is:

`y=mx+b`

Where m is the slope and b is the y-intercept.

The slope is the rate and y-intercept is the starting point.

Let's re-arrange our equation in this form:

`\begin{gathered} L=15-1.5t \\ L=-1.5t+15 \end{gathered}`

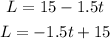
So, we can see that the slope is -1.5 and y-intercept is 15.

### What is the slope of the equation and what is its interpretation in the context of the problem?

The slope is -1.5 and it means that the candle burns 1.5 inches per hour.

Answer

The slope of the function is - 1.5 which reveals the number of inches of candle that burns per hour.