Answer:
The average speed is greater than the magnitude average velocity because the total distance is greater than the displacement of the man.
Step-by-step explanation:
First, let's write 2h 14 min as a decimal, so:
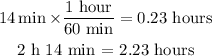
Now, the average velocity is equal to the division of the displacement by time. The displacement is the straight-line distance, so the average velocity is:
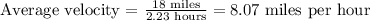
On the other hand, the average speed is the division of the total distance by time, so the average speed is:
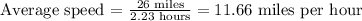
Therefore, the average speed is greater than the magnitude average velocity because the total distance is greater than the displacement of the man.