For this question we need to use the formula for compound interest:
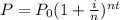
Where P is the final value, P0 is the initial value, i is the interest rate, t is the time in years and n is a value that depends on the compound rate (let's assume that is monthly, so we have n = 12)
Calculating the principal (P0) for account A, using the interest (P - P0) equal 27, we have:

So the principal for account A is $244.90.
For account B, we have:
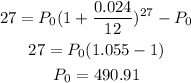
The principal for account B is $490.91.