Question

I just have one question, in the parabola y=(x+1)^2-5, to find the vertex, how come when using the equation y=(x-h)^2+k, Aleks goes from (x+1)^2-5 to y=(x-(-1)^2+(-5), and they place a negative 1 in the parentheses instead of a positive one like in the original parabola?

Answer 1

The general equation of parabola wit vertex (h,k) is,

`y=(x-h)^2+k`

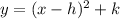
Simplify the equation of parabola in standard form.

`\begin{gathered} y=(x+1)^2-5 \\ =\lbrack x-(-1)\rbrack^2-5 \end{gathered}`

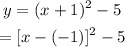
Compare the parabola equation with general equation to obtain the vertex of parabola. So, vertex of given parabola is (-1,-5).

Consider two values of x to the right of -1 and two value to the left of -1.

For x = -2,

`\begin{gathered} y=(-2+1)^2-5 \\ =1-5 \\ =4 \end{gathered}`

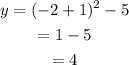
For x = -4,

`\begin{gathered} y=(-4+1)^2-5 \\ =9-5 \\ =4 \end{gathered}`

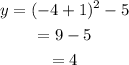
For x = 0,

`\begin{gathered} y=(0+1)^2-5 \\ =1-5 \\ =-4 \end{gathered}`

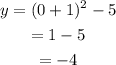
For x = 2;

`\begin{gathered} y=(2+1)^2-5 \\ =9-5 \\ =4 \end{gathered}`

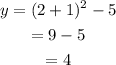
Plot the parabola on the graph and mention the points on the parabola.