Question

Find the slope of the line passing through the points (-4, -3) and (8, -9).8 08UndefinedХ5?

Answer 1

`y(x)=-(1)/(2)x-5`

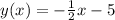
Step-by-step explanation: We have to find the standard equation of a line that passes through the two points, (-4,-3) and (8,-9):

The stand line equation:

`\begin{gathered} y(x)=mx+b\Rightarrow(1) \\ m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1) \end{gathered}`

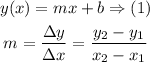
The slope and the y-intercept of the equation are determined as follows:

`\begin{gathered} (x_1,y_1)=(-4,-3) \\ (x_2,y_2)=(8,-9) \end{gathered}`

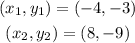
The slope:

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1))=(-9-(-3))/(8-(-4)) \\ m=(-9-(-3))/(8-(-4))=(-6)/(12) \\ m=-(1)/(2) \end{gathered}`

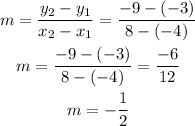
y-intercept:

`\begin{gathered} y(x)=-(1)/(2)x+b \\ (x,y)=(-4,-3) \\ -3=-(1)/(2)(-4)+b \\ -3=2+b \\ b=-5 \end{gathered}`

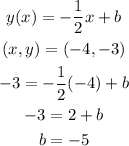
The equation finally is as follows:

`y(x)=-(1)/(2)x-5\Rightarrow(2)`

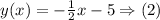
The plot:

Follwoing plot confirms that the equation passes through the points (-4,-3) and (8,-9):