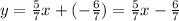Question

7. Consider the line below.A. Find two points on this line with whole number coordinates.B. Find an equation for this line in point slope form,C. Find the equation for this line in slope intercept form. Be sure to show your work-50

Answer 1

Just a reminder:

The slope-intercept form of a linear equation is:

y=mx+b; where m is the slope of the line and b its intersection with the y axis

On the other hand, the point-slope equation is:

`y-y_1=m(x-x_1)`

Where (x_1, y_1) is a point in the line

So, (besides the blindness of the tutor) we can identify that the points we are looking for in part a) are:

`(-3,-3)and(4,2)`

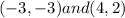
You can notice that by the fact that the line goes exactly through those two points in particular, so that's the answer to part a)

As for part b)

Remember that we can calculate the slope using the formula:

`m=(\mleft(y_2-y_1\mright))/((x_2-x_1))`

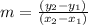
And using the 2 points found in part a)

`m=((-3-(2)))/((-3-(4)))=(-5)/(-7)=(5)/(7)`

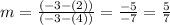
Then,

`y-2=(5)/(7)(x-4);\text{ point-slope equation}`

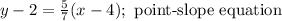
We used (x_1,y_1)= (4,2) in this part

Finally, regarding part C:

Notice that using the equation found in part b, when x=0

`y-2=(5)/(7)(0-4)=(5)/(7)(-4)\Rightarrow y=2-(20)/(7)=-(6)/(7)`

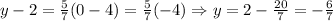
So, our solution to part C is:

`y=(5)/(7)x+(-(6)/(7))=(5)/(7)x-(6)/(7)`