Question

Question 7 of 10What is the length of CD? In this diagram, AABC ~ AEDC.20-XX21AO A. 6OB. 3C. 4D. 5SUBMIT

Answer 1

The triangles ABC and EDC are similar which means that the rate between corresponding sides is equal, so that:

`(EC)/(AC)=(DC)/(BC)`

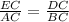
We know that

EC=7

AC=21

DC=x

BC=20-x

`\begin{gathered} (7)/(21)=(x)/(20-x) \\ (1)/(3)=(x)/((20-x)) \end{gathered}`

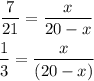
First, you have to multiply both sides by (20-x) to take the x-term from the denominator's place

`\begin{gathered} (1)/(3)(20-x)=(20-x)(x)/(20-x) \\ (1)/(3)(20-x)=x \end{gathered}`

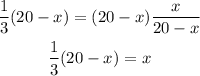
Next, distribute the multiplication on the parentheses term:

`\begin{gathered} (1)/(3)\cdot20-(1)/(3)\cdot x=x \\ (20)/(3)-(1)/(3)x=x \end{gathered}`

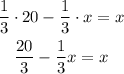
And pass the x-term to the right side of the equation by applying the opposite operation

`\begin{gathered} (20)/(3)-(1)/(3)x+(1)/(3)x=x+(1)/(3)x \\ (20)/(3)=(4)/(3)x \end{gathered}`

Finally multiply both sides of the expression by the reciprocal fraction of 4/3, i.e. the inverse fraction

`\begin{gathered} (20)/(3)\cdot(3)/(4)=((4)/(3)\cdot(3)/(4))x \\ 5=x \end{gathered}`

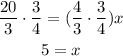
x=5 → so the length of CD is 5 units.

The correct option is D.