By definition, a Rotation is a transformation in which a figures is turned about a Center of rotation.
It is important to remember that, in transformations, the Image is the figure obtained after the transformation and the Pre-Image is the original figure.
In this case, you can identify that the vertices of the Pre-Image STU have the following coordinates:
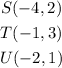
And the coordinates of the vertices of its Image, are:

Notice that the coordinates of the Image are obtained by multiplying the coordinates of the Pre-Image by -1.
By definition, when you rotate a figure 180° about the Origin, the rule is:

Therefore, the answer is: Option B.