Question

A 6 meter beam with 4 meters of its length extended over the edge of a building. A 1000 newton man stands onthe edge of the 600 newton beam to keep it from falling over the edge of the building. How far from the building'sedge can a 400 newton kid walk without causing the whole system to flip over the edge?

Answer 1

The distance of the mass of 1000 N weight from the edge is,

`d=6\text{ m}`

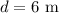
The distance of the center of the beam from the edge is,

`\begin{gathered} D=(6)/(2) \\ D=3\text{ m} \end{gathered}`

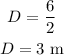
Due to the weight of the man of 1000 N standing on the beam and building, there is normal force acting at the distance of 6 m from the edge of the beam in upward direction.

The weight of the beam and the kid is in downward direction.

Let the distance of the kid from the edge is x.

The net moment about the edge must be zero, so that the beam does not fall.

Thus,

`\begin{gathered} -1000*4+600*3+400* x=0 \\ -4000+1800+400x=0 \\ -2200+400x=0 \\ 400x=2200 \\ x=(2200)/(400) \\ x=5.5\text{ m} \end{gathered}`

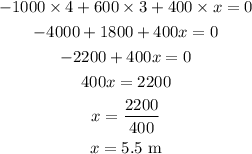
Thus, the distance of the kid from the left edge till where the beam cannot fall is 5.5 m .