Question

If m 2 = 40 what is the measure of 1 + 6

Answer 1

`\angle1\text{ + }\angle6\text{ = 280}`

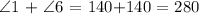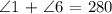
Here, we want to get the measure of the sum of angles labeled 1 and 6

From the question, we can see that angle 1 and 2 lies on the same horizontal line. Angles on a straight line are supplementary, which means they add up to 180

Mathematically;

`\begin{gathered} \angle1\text{ + }\angle2\text{ = 180} \\ \angle1\text{ + 40 = 180} \\ \angle1\text{ = 180-40} \\ \angle1\text{ = 140} \end{gathered}`

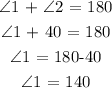
As we can see from the diagram, angles 1 and 6 are vertically opposite angles. Mathematically, vertically opposite angles are equal. That means the measure of angle 6 too is 140

Thus, we have their sum as follows;

`\angle1\text{ + }\angle6\text{ = 140+140 = 280}`