Question

If a game consists of picking a number from a bag of beans numbered 2, 2, 3, 4, and 5 and flipping a coin, which probabilities are equivalent?I. P(2 and head)II. P(even and tail) III. P(odd and tail) A) I and IIB) I and IIIC) II and IIID) none of the above

Answer 1

B) I and III

Explanation:

Given:

• A bag of beans numbered 2, 2, 3, 4, and 5.

,

• A coin

To determine which probabilities are equivalent, we calculate the probabilities in I, II, and III below,

Part I

`\begin{gathered} P(selecting\text{ a bean numbered 2)}=(2)/(5) \\ P(flipping\; a\; head\text{)}=(1)/(2) \\ \implies P(2\text{ and head)}=(2)/(5)*(1)/(2)=(1)/(5) \end{gathered}`

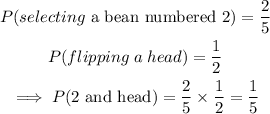
The probability of picking a 2 and flipping a head is 1/5.

Part II

`\begin{gathered} P(selecting\text{ an even nu}mbered\; bean\text{)}=(3)/(5) \\ P(flipping\; a\; tail\text{)}=(1)/(2) \\ \implies P(even\text{ and tail)}=(3)/(5)*(1)/(2)=(3)/(10) \end{gathered}`

The probability of picking an even numbered bean and flipping a tail is 3/10.

Part III

`\begin{gathered} P(selecting\text{ an odd nu}mbered\; bean\text{)}=(2)/(5) \\ P(flipping\; a\; tail\text{)}=(1)/(2) \\ \implies P(odd\text{ and tail}=(2)/(5)*(1)/(2)=(1)/(5) \end{gathered}`

The probability of picking an odd-numbered bean and flipping a tail is 1/5.

The equivalent probabilities are I and III. (Option B is correct).