Determine the mean of the data.
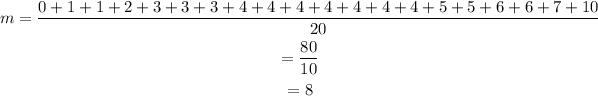
Mean of the data is 8.
In the data number 4 occured most number of time so mode value of this data is 4.
Arrange the number in ascending order,
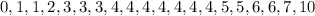
There are 20 observations in the data. So average of (20/2)th term and (20/2 +1 )term in arranged series given the median value of data.
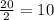
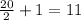
The 10th term in the arranged data is 4 and 11th term in the data is 4.
Determine the average of 10th and 11th term of the data.
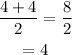
So median value is 4.