Question

What are the coordinates of the foci for this ellipse?

Answer 1

From the attached picture we can see an ellipse of

center (2, -3)

Vertices (2, 2) and (2, -8)

C-vertices (-1, -3) and (5, -3)

Since the coordinates of the center are (h, k), then

`\begin{gathered} h=2 \\ k=-3 \end{gathered}`

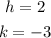
Since the coordinates of the vertices are (h, k + a), (h, k - a), then

`\begin{gathered} k+a=2 \\ -3+a=2 \\ a=2+3 \\ a=5 \end{gathered}`

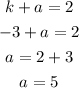
Since the coordinates of the co-vertices are (h + b, k) and (h - b, k), then

`\begin{gathered} h+b=5 \\ 2+b=5 \\ b=5-2 \\ b=3 \end{gathered}`

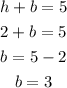
Since the coordinates of the foci are (h, k + c) and (h, k - c)

To find c use the relation

`\begin{gathered} c^2=a^2+b^2 \\ c^2=5^2+3^2 \\ c^2=25+9 \\ c^2=34 \\ c=\pm\sqrt[]{34} \end{gathered}`

Then the foci are

`(2,-3+\sqrt[]{34})\text{ \& (2, -3-}\sqrt[]{34})`

The correct answer is C (3rd choice)