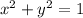Question

I need help with steps on how to solve this

Answer 1

The equation relating x and y is;

`x^2+y^2=1`

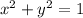
Step-by-step explanation:

Given the circle of radius 1 unit centered at the origin.

Recall that the equation of circle can be written as;

`(x-h)^2+(y-k)^2=r^2`

Where;

`\begin{gathered} (h,k)=the\text{ center of the circle} \\ (h,k)=(0,0)\text{ Origin} \\ r\text{ = radius =1 unit} \end{gathered}`

substituting we have;

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-0)^2+(y-0)^2=1^2 \\ x^2+y^2=1 \end{gathered}`

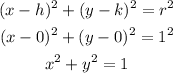
Graphing the circle, we have;

Applying Pythagorean Theorem;

Applying Pythagorean theorem to solve for x and y;

`\begin{gathered} a^2+b^2=c^2 \\ \text{substituting;} \\ x^2+y^2=1^2 \\ x^2+y^2=1 \end{gathered}`

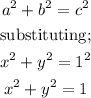
The equation relating x and y is;

`x^2+y^2=1`