Question

A mass M1=6kg rests on a frictionless table and connected by a massless string over a massless pulley to another mass M2=6.8kg which hangs freely from the string. When released, the hanging mass falls a distance d=.9m.1) How much work is done by the normal force on M1?2) What is the final speed of the two blocks?3) How much work is done by tension on M1?4) What is the tension in the string as the block falls?5) The work done by tension on only M2 is? a) positive b) zero, c) negative.6) What is the NET work done on M2?

Answer 1

Given data:

* The mass on the frictionless table is,

`m_1=6\text{ kg}`

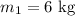
* The mass hangs freely from the string is,

`m_2=6.8\text{ kg}`

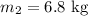
* The hanging mass falls a distance is,

`d=0.9\text{ m}`

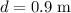
Solution:

(1). The normal force of mass on the frictionless table is,

`\begin{gathered} F_N=m_1g \\ F_N=6*9.8 \\ F_N=58.8\text{ N} \end{gathered}`

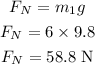
As the displacement of the mass m_1 on the frictionless table is in the hroizontal direction.

Thus, the work done by teh normal force is,

`W=F_Nd\cos (\theta)`
`\text{where }\theta\text{ is the angle between the normal force and dispalcement}`

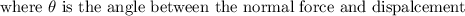
As both the normal force and displacement are perpendicuular to each other.

Thus, the work done by the nromal force on the mass m_1 is,

`\begin{gathered} W=F_Nd\cos (90^(\circ)) \\ W=0 \end{gathered}`

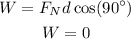
Thus, the work done by the normal force on m_1 is zero.