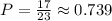You have the next set: Total of marbles in the bag:
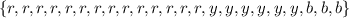
Where r is red marble, y is yellow marble and b is blue marble.
Yu have in total 23 marble in the bag.
T=23
The next set is the marble that are red or blue:

Then, 17 marble are red or blue.
Then, the probability of drawn from the bag a marble red or blue is: Approximate 0.74