We have got 10 invitations, 4 are i blue paper, so 6 are not in blue paper.
To find the probability, we will calculate how many combinations are there and how many combination in which exactly 2 out of 5 of the invitations are blue.
The total combinations of the 5 are just 10! over 5!:
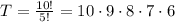
The combinations of ecatly 2 blue starts with 4*3/2!, becase initially we have 4 to choose from but the second we have one less. Now we multiply by the same for the non blue, so 6*5*4/3!, and we get:

The probability is the combinations of the event we want, B, divided by the total combinations, T:

So, the probability that exactly 2 of the choosen invitations are printed in blue is 0.0040.