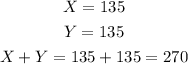We have the following:
We have that the cosine and the sine are equal their quotient, that is, tangent, is 1. And this happens when the angle is 45 degrees.
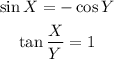
We know that the second quadrant (between 90 and 180 degrees), the sine is negative and the cosine is positive, therefore, in 135 (90 + 45) degree it will be -1.
Therefore the answer is: