1 Answer

Drastega · Answer 1 · 2023-07-11T07:33:46+0000

We know a quadratic function in standard form is given by:

where a, b and c are constants. To find the value of the constants we can use the points given.

For the point (-2,65) we have:

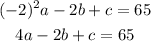
$\begin{gathered} (-2)^2a-2b+c=65 \\ 4a-2b+c=65 \end{gathered}$

For the point (0,165) we have:

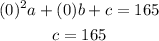
$\begin{gathered} (0)^2a+(0)b+c=165 \\ c=165 \end{gathered}$

For the point (6,225) we have:

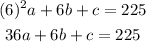
$\begin{gathered} (6)^2a+6b+c=225 \\ 36a+6b+c=225 \end{gathered}$

Hence we have the system of equations:

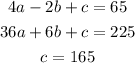
$\begin{gathered} 4a-2b+c=65 \\ 36a+6b+c=225 \\ c=165 \end{gathered}$

Plugging the value of c in the first two equations we have:

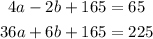
$\begin{gathered} 4a-2b+165=65 \\ 36a+6b+165=225 \end{gathered}$

which leads to:

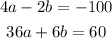
$\begin{gathered} 4a-2b=-100 \\ 36a+6b=60 \end{gathered}$

Multiplying the first equation by 3 we have:

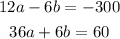
$\begin{gathered} 12a-6b=-300 \\ 36a+6b=60 \end{gathered}$

adding the equations we have that:

$\begin{gathered} 48a=-240 \\ a=-(240)/(48) \\ a=-5 \end{gathered}$

Plugging the value of a in the equation above we have:

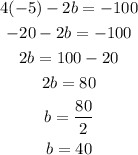
$\begin{gathered} 4(-5)-2b=-100 \\ -20-2b=-100 \\ 2b=100-20 \\ 2b=80 \\ b=(80)/(2) \\ b=40 \end{gathered}$

Once we know the values of the constants we conclude that the quadratic equation in standard form is:

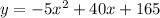
Now, to write the equation in vertex form we need to complete the square on x:

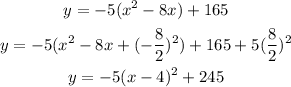
$\begin{gathered} y=-5(x^2-8x)+165 \\ y=-5(x^2-8x+(-(8)/(2))^2)+165+5((8)/(2))^2 \\ y=-5(x-4)^2+245 \end{gathered}$

Therefore, the equation written in vertex form is:

Now, the unique features of the two forms presented are:

Standard form: The equation is expanded and reduced.

Vertex form: The vertex of the parabola is readily shown in the equation.

Please log in or register to add a comment.