To determine the accrued amount on a savings account that earns an annual simple interest, you have to use the following formula:
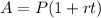
Where
A is the accrued amount after a determined time period
P is the principal or initial amount in the account
r is the interest rate, expressed as a decimal value
t is the time period, expressed in years
The initial amount of the account was $2300.
The time period was 10 years.
The interest rate is R=5.5%, to express it as a decimal value you have to divide it by 100:
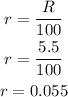
Replace the known values in the formula to determine the accrued amount:
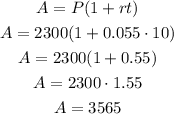
Now, the accrued amount (A) is equal to the sum of the initial amount (P) and the interest (I) earned after t time periods:
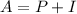
To determine the interest earned, you can subtract the initial amount from the accrued amount
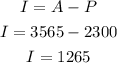
So, after 10 years she earned $1265 of interest.