Step-by-step explanation:
To know the new coordinates for F', G', and H', we need to follow the rule, so:
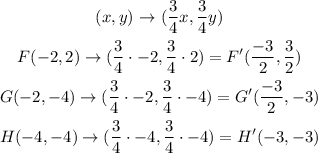
Then, to reflect over the x-axis, we need to use the following rule:
(x, y) ---> (x, -y)
So, the new coordinates F'', G'', and H" after the reflection are:
F'(-3/2, 3/2) ----> F"(-3/2, -3/2)
G'(-3/2, -3) -----> G"(-3/2, 3)
H'(-3, -3) --------> H"(-3, 3)
Therefore, the graph of figure F"G"H" is: