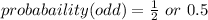Step-by-step explanation:
The ste of numbers on the 14 sided die is given below as
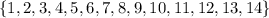
The total sample space is given below as
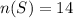
The set of required out comes which is the odd numbers is given below as
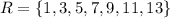
the number of required outcomes is given below as
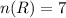
To calculate the probability ofrolling an odd number, we will use the formula below

By substituting the values, we will have

Hence,
The final answer is