Question

Given BC ≅ BA, CD ≅ ADProve ΔABD ≅ ΔCBD

Answer 1

The triangles ΔABD and ΔCBD share one common side, BD. Since they share this side, it has the same measure for both triangles.

Since it is given that

`\begin{gathered} BC\cong BA \\ CD\cong AD \end{gathered}`

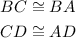
The SSS(Side-Side-Side) congruence postulate states that If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.

Thus, by the SSS Postulate

`\Delta ABD\cong\Delta CBD`

Since the problem wants us to write this proof as a two column proof, first we need to understand what this is. A two column proof is a table where the left column contains a statement, and the corresponding line on the right column has its reason to be a true statement.

We start with the following statements

`\begin{gathered} BC\cong BA \\ CD\cong AD \end{gathered}`

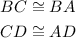
They are true because they are given.

Then, we have

`BD\cong DB`

They are congruent because they are the same segment.

And finally,

`\Delta ABD\cong\Delta CBD`

This statement is true because combining the previous statements we can apply the SSS Congruence Postulate.