Question

Suppose a company has fixed costs of $350 and variable cost of (0.49x + 1160) dollars per item.Suppose the selling price is (-0.51x+1340) dollars per unit.Find the cost function. C(x) =Find the revenue function. R(x) =Find the profit function. P(x) =

Answer 1

We have a fixed cost of $350 and a unit variable cost of 0.49x+1160.

We then can express the cost function as the sum of the fixed cost and variable cost:

`\begin{gathered} C(x)=FC+VC \\ C(x)=350+(0.49x+1160)x \\ C(x)=350+0.49x^2+1160x \\ C(x)=0.49x^2+1160x+350 \end{gathered}`

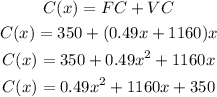
The revenue function R(x) can be expressed as the selling price, -0.51x+1340, times the quantity, x:

`\begin{gathered} R(x)=P(x)\cdot x \\ R(x)=(-0.51x+1340)x \\ R(x)=-0.51x^2+1340x \end{gathered}`

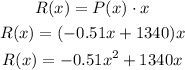
The profit function P(x) can be expressed as the revenue R(x) minus the cost C(x):

`\begin{gathered} P(x)=R(x)-C(x) \\ P(x)=(-0.51x^2+1340x)-(0.49x^2+1160x+350) \\ P(x)=-0.51x^2+1340x-0.49x^2-1160x-350 \\ P(x)=(-0.51-0.49)x^2+(1340-1160)x-350 \\ P(x)=-x^2+180x-350 \end{gathered}`

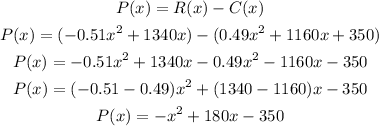
Answer:

C(x) = 0.49x² + 1160x +350

R(x) = -0.51x² + 1340x

P(x) = -x² + 180x - 350