Question

Determine whether the lines are parallel, intersect, or coincidingY= 1/3x + 4X - 3y = -12

Answer 1

So, we want to determine whether the lines:

`\begin{gathered} y=(1)/(3)x+4 \\ x-3y=-12 \end{gathered}`

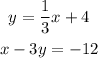
First, remember that there are two different ways to represent a line with an equation. These are:

`y=mx+b`

Where m is the slope.

For example:

`y=(1)/(3)x+4`

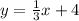
Where the slope is 1/3.

The second way, has the equation of the form:

`Ax+By+C=0`

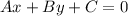
Where the slope is given by the operation:

`(-A)/(B)`

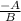
For example:

`x-3y+12=0`

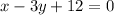
Where the slope is:

`(-(1))/(-3)=(1)/(3)`

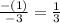
As you can see, both lines has the same slope, so, they are parallel.

Remember!

- Two lines are parallel if they have the same slope.

- Two lines are perpendicular if the product of their slopes is -1.