Question

suppose that grade point averages of undergraduate students at one university have a bell shaped distribution with a mean of 2.61 and a standard deviation of 0.45.Using the empirical rule, what percentage of the students have grade point averages that are at least 2.16? Please do not round your answer?

Answer 1

Step 1:

Write the given data

`\begin{gathered} mean(\mu)=2.61\text{ } \\ s\text{tandard deviation }\sigma\text{ = 0.45} \end{gathered}`

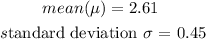
Step 2

Write the z-score formula

`z\text{ = }\frac{\text{x - }\mu}{\sigma}`

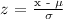
Step 3

The Empirical rule formula states that

1) 68% of data falls within 1 standard deviation from the mean - that means between μ - σ and μ + σ.

2) 95% of data falls within 2 standard deviations from the mean - between μ – 2σ and μ + 2σ.

3) 99.7% of data fall within 3 standard deviations from the mean - between μ - 3σ and μ + 3σ.

Step 4

We start with the first rule

1) 68% of data falls within 1 standard deviation from the mean - that means between μ - σ and μ + σ.

μ - σ = 2.61 - 0.45 = 2.16

μ + σ = 2.61 + 0.45 = 3.06

Finally from the 1st rule, we can see that 68% of the students have grades that fall between 2.16 and 3.06.

The question asks us to find the percentage of students that have grade points that are at least 2.16

This means students with grade points equal to or greater that 2.16(≥)

`.`

Hence,

For students with grade points = 2.16

= 68%

For students with grade points of more than 2.16

`\begin{gathered} \frac{100\text{ - 68}}{2}\text{ \%} \\ \text{= }(32)/(2) \\ \text{= 16\%} \end{gathered}`

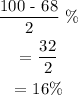
Therefore, the percentage of the students who have grade point averages that are at least 2.16 is

= 68% + 16%

= 84%