Question

Suppose a comet orbits the Sun every 84 years and has an eccentricity of 0.96. What is the length of its semi-major axis in AU?

Answer 1

We are given that a comet has a period of 84 years. We are asked to determine the length of its semi-major axis. To do that we will use the following formula:

`p^2=a^3`

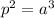
This is Kepler's third law, where:

`\begin{gathered} p=\text{period} \\ a=\text{ distance to semi-major ax}is \end{gathered}`

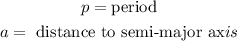
Now, we solve for "a" by taking the cubic root to both sides:

`\sqrt[3]{p^2}=a`

Now we substitute the value of 84 years:

`\sqrt[3]{(84)^2}=a`

Solving the operations:

`19.2AU=a`

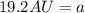
Therefore, the length of the semi-major axis is 19.2 Astronomical Units.