Question

Select the correct answer.What is the solution to the equation?(1 - 2)2 + 4 = 1-Ο Α.-3 and -6OB.3 and 6O C. -3OD. 6ResetNext

Answer 1

Given the equation:

`\mleft(x-2\mright?^{})^{(1)/(2)}+4=x`

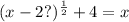
1. You need to remember the following property:

`\sqrt[n]{b^m}=b^{(m)/(n)}`

2. Then, you can rewrite the equation as follows:

`\sqrt[]{x-2}^{}+4=x`

3. Now you need to apply the Subtraction Property of Equality by subtracting 4 from both sides of the equation:

`\begin{gathered} \sqrt[]{x-2}^{}+4-(4)=x-(4) \\ \\ \sqrt[]{x-2}^{}=x-4 \end{gathered}`

4. Square both sides of the equation:

`\begin{gathered} (\sqrt[]{x-2})^{}=(x-4)^2 \\ x-2=(x-4)^2 \end{gathered}`

5. Apply the following on the right side:

`(a-b)^2=a^2-2ab+b^2`

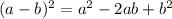
Then:

`\begin{gathered} x-2=(x^2-2(x)(4)+4^2) \\ \\ x-2=x^2-8x+16 \end{gathered}`

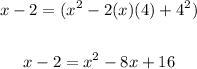
6. Write the Quadratic Equation in this form:

`ax^2+bx+c=0`

Then:

`\begin{gathered} 0=x^2-8x+16-x+2 \\ x^2-9x+18=0 \end{gathered}`

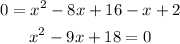
7. In order to factor it, you can find two numbers whose sum is -9 and whose product is 18. These numbers would be -3 and -6. Then:

`(x-3)(x-6)=0`

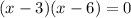
8. Notice that you get these values of "x":

`\begin{gathered} x-3=0\Rightarrow x_1=3 \\ \\ x-6=0\Rightarrow x_2=6_{} \end{gathered}`

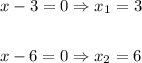
9. Substitute each value of "x" into the equation and evaluate, in order to check if they are solutions to the equation:

- For:

`x_1=3`

You get:

`\begin{gathered} \sqrt[]{(3)-2}^{}+4=(3) \\ \sqrt[]{1}^{}+4=3 \\ 5=3\text{ (False)} \end{gathered}`

It is not a solution.

- For:

`x_2=6`

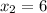
You get:

`\begin{gathered} \sqrt[]{(6)-2}^{}+4=(6) \\ \sqrt[]{4}+4=6 \\ 2+4=6 \\ 6=6\text{ (True)} \end{gathered}`

It is a solution.

Hence, the answer is: